Examples
It is the final part of the Multivariate Kalman Filter chapter.
It includes two numerical examples. In the first example, we design a six-dimensional Kalman Filter without control input. In the second example, we design a two-dimensional Kalman Filter with a control input.
Example 9 – vehicle location estimation
In the following example, we implement the Multivariate Kalman Filter using the material we've learned.

In this example, we estimate the vehicle's location on the \( XY \) plane.
The vehicle has an onboard location sensor that reports \( X \) and \( Y \) coordinates of the system.
We assume constant acceleration dynamics.
The state extrapolation equation
First, we derive the state extrapolation equation. As you remember, the general form of the state extrapolation equation in matrix notation is:
| \( \boldsymbol{\hat{x}}_{n+1,n} \) | is a predicted system state vector at time step \( n + 1 \) |
| \( \boldsymbol{\hat{x}}_{n,n} \) | is an estimated system state vector at time step \( n \) |
| \( \boldsymbol{u}_{n} \) | is a control variable |
| \( \boldsymbol{w}_{n}\) | is the process noise |
| \( \boldsymbol{F} \) | is the state transition matrix |
| \( \boldsymbol{G} \) | is the control matrix |
In this example, there is no control variable \( \boldsymbol{u} \) since there is no control input.
For this example, the state extrapolation equation can be simplified to:
\[ \boldsymbol{\hat{x}}_{n+1,n} = \boldsymbol{F\hat{x}}_{n,n} \]
The system state \( \boldsymbol{x}_{n} \) is defined by:
\[ \boldsymbol{x}_{n}= \left[ \begin{matrix} x_{n}\\ \dot{x}_{n}\\ \ddot{x}_{n}\\ y_{n}\\ \dot{y}_{n}\\ \ddot{y}_{n}\\ \end{matrix} \right] \]
The extrapolated vehicle state for time \( n + 1 \) can be described by the following system of equations:
\[ \begin{cases} \hat{x}_{n+1,n} = \hat{x}_{n,n} + \hat{\dot{x}}_{n,n} \Delta t+ \frac{1}{2}\hat{\ddot{x}}_{n,n}\Delta t^{2}\\ \hat{\dot{x}}_{n+1,n} = \hat{\dot{x}}_{n,n} + \hat{\ddot{x}}_{n,n}\Delta t\\ \hat{\ddot{x}}_{n+1,n} = \hat{\ddot{x}}_{n,n}\\ \hat{y}_{n+1,n} = \hat{y}_{n,n} + \hat{\dot{y}}_{n,n} \Delta t+ \frac{1}{2}\hat{\ddot{y}}_{n,n}\Delta t^{2}\\ \hat{\dot{y}}_{n+1,n} = \hat{\dot{y}}_{n,n} + \hat{\ddot{y}}_{n,n}\Delta t\\ \hat{\ddot{y}}_{n+1,n} = \hat{\ddot{y}}_{n,n} \end{cases} \]
In matrix form:
\[ \left[ \begin{matrix} \hat{x}_{n+1,n}\\ \hat{\dot{x}}_{n+1,n}\\ \hat{\ddot{x}}_{n+1,n}\\ \hat{y}_{n+1,n}\\ \hat{\dot{y}}_{n+1,n}\\ \hat{\ddot{y}}_{n+1,n}\\ \end{matrix} \right] = \left[ \begin{matrix} 1 & \Delta t & 0.5\Delta t^{2} & 0 & 0 & 0\\ 0 & 1 & \Delta t & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & \Delta t & 0.5\Delta t^{2}\\ 0 & 0 & 0 & 0 & 1 & \Delta t\\ 0 & 0 & 0 & 0 & 0 & 1\\ \end{matrix} \right] \left[ \begin{matrix} \hat{x}_{n,n}\\ \hat{\dot{x}}_{n,n}\\ \hat{\ddot{x}}_{n,n}\\ \hat{y}_{n,n}\\ \hat{\dot{y}}_{n,n}\\ \hat{\ddot{y}}_{n,n}\\ \end{matrix} \right] \]
The covariance extrapolation equation
The general form of the Covariance Extrapolation Equation is given by:
| \( \boldsymbol{P}_{n,n} \) | is the covariance matrix of the current state estimation |
| \( \boldsymbol{P}_{n+1,n} \) | is the covariance matrix of the next state estimation (prediction) |
| \( \boldsymbol{F} \) | is the state transition matrix that we've derived in "Modeling linear dynamic systems" section |
| \( \boldsymbol{Q} \) | is the process noise matrix |
The estimate covariance matrix is:
\[ \boldsymbol{P} = \left[ \begin{matrix} p_{x} & p_{x\dot{x}} & p_{x\ddot{x}} & p_{xy} & p_{x\dot{y}} & p_{x\ddot{y}} \\ p_{\dot{x}x} & p_{\dot{x}} & p_{\dot{x}\ddot{x}} & p_{\dot{x}y} & p_{\dot{x}\dot{y}} & p_{\dot{x}\ddot{y}} \\ p_{\ddot{x}x} & p_{\ddot{x}\dot{x}} & p_{\ddot{x}} & p_{\ddot{x}y} & p_{\ddot{x}\dot{y}} & p_{\ddot{x}\ddot{y}} \\ p_{yx} & p_{y\dot{x}} & p_{y\ddot{x}} & p_{y} & p_{y\dot{y}} & p_{y\ddot{y}} \\ p_{\dot{y}x} & p_{\dot{y}\dot{x}} & p_{\dot{y}\ddot{x}} & p_{\dot{y}y} & p_{\dot{y}} & p_{\dot{y}\ddot{y}} \\ p_{\ddot{y}x} & p_{\ddot{y}\dot{x}} & p_{\ddot{y}\ddot{x}} & p_{\ddot{y}y} & p_{\ddot{y}\dot{y}} & p_{\ddot{y}} \\ \end{matrix} \right] \]
The elements on the main diagonal of the matrix are the variances of the estimation:
- \( p_{x} \) is the variance of the \( X \) coordinate position estimation
- \( p_{\dot{x}} \) is the variance of the \( X \) coordinate velocity estimation
- \( p_{\ddot{x}} \) is the variance of the \( X \) coordinate acceleration estimation
- \( p_{y} \) is the variance of the \( Y \) coordinate position estimation
- \( p_{\dot{y}} \) is the variance of the \( Y \) coordinate velocity estimation
- \( p_{\ddot{y}} \) is the variance of the \( Y \) coordinate acceleration estimation
- The off-diagonal entries are covariances
We assume that the estimation errors in \( X \) and \( Y \) axes are not correlated so that the mutual terms can be set to zero.
Example analysis
The following chart demonstrates the KF location and velocity estimation performance.
The chart on the left compares the true, measured, and estimated values of the vehicle position. Two charts on the right compare the true, measured, and estimated values of \( x \)-axis velocity and \( y \)-axis velocity.
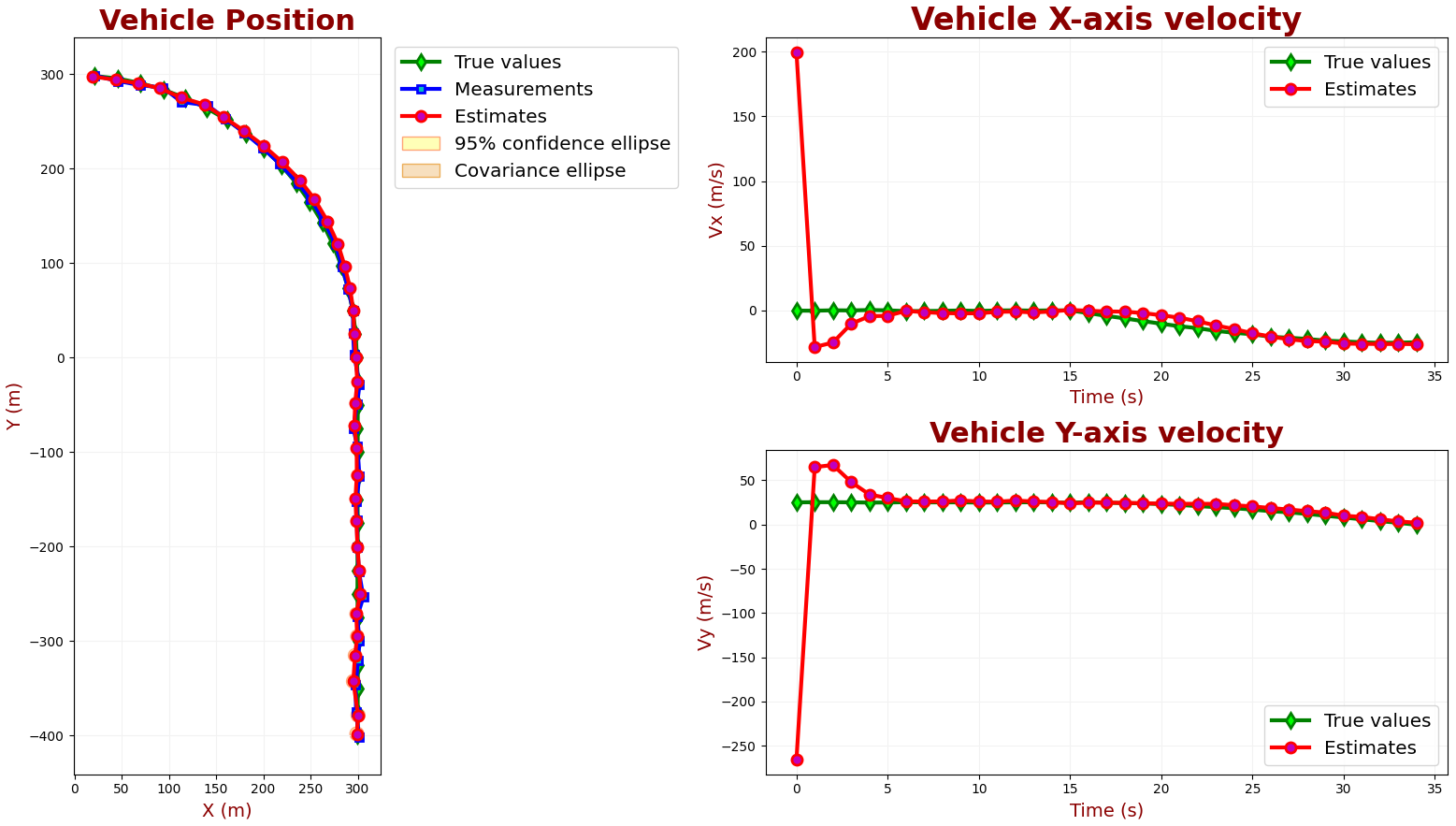
As you can see, the Kalman Filter succeeds in tracking the vehicle.
Let us zoom the linear part of the vehicle motion and the turning maneuver part.
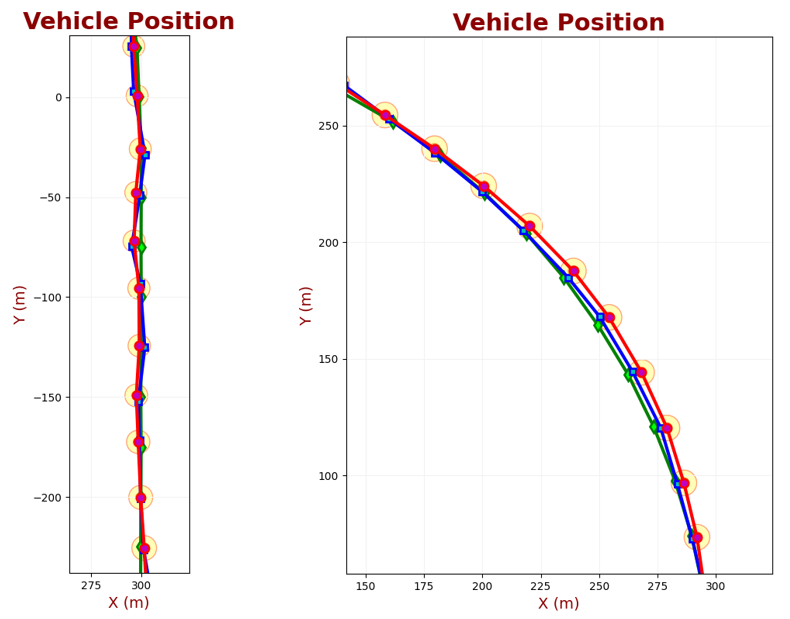
The circles on the plot represent the 95% confidence ellipse. Since the \( x \) and \( y \) axes' measurement errors are equal, the confidence ellipse is a circle.
While the vehicle travels along a straight line, the acceleration is constant and equal to zero. However, during the turn maneuver, the vehicle experiences acceleration due to the circular motion - angular acceleration.
Recall from an introductory physics that angular acceleration is \( \alpha = \frac{\Delta V}{R \Delta t} \) , where \( \Delta t \) is the time interval, \( \Delta V \) is the velocity difference within the time interval, and \( R \) is the circle radius.
Although the angular acceleration is constant, the angular acceleration projection on the \( x \) and \( y \) axes is not constant, therefore \( \ddot{x} \) and \( \ddot{y} \) are not constant.
Our Kalman Filter is designed for a constant acceleration model. Nevertheless, it succeeds in tracking maneuvering vehicle due to a properly chosen \( \sigma_{a}^{2} \) parameter.
Example 10 – rocket altitude estimation
In this example, we estimate the altitude of a rocket. The rocket is equipped with an onboard altimeter that provides altitude measurements. In addition to an altimeter, the rocket is equipped with an accelerometer that measures the rocket's acceleration.
The accelerometer serves as a control input to the Kalman Filter.
We assume constant acceleration dynamics.
Accelerometers measurements include gravitational acceleration. An accelerometer at rest on a table measures \( 1g \) upwards, while an accelerometer in free fall measures zero acceleration. Thus, we need to subtract the gravitational acceleration constant \( g \) from each accelerometer measurement.
The accelerometer measurement at time step \( n \) is:
\[ a_{n} = \ddot{x} - g + \epsilon \]
Where:
- \( \ddot{x} \) is the actual acceleration of the object (the second derivative of the object position)
- \( g \) is the gravitational acceleration constant; \( g = -9.8\frac{m}{s^{2}} \)
- \( \epsilon \) is the accelerometer measurement error
The state extrapolation equation
The general form of the state extrapolation equation in matrix notation is:
| \( \boldsymbol{\hat{x}}_{n+1,n} \) | is the predicted system state vector at time step \( n + 1 \) |
| \( \boldsymbol{\hat{x}}_{n,n} \) | is the estimated system state vector at time step \( n \) |
| \( \boldsymbol{u}_{n} \) | is the control variable |
| \( \boldsymbol{w}_{n} \) | is the process noise |
| \( \boldsymbol{F} \) | is the state transition matrix |
| \( \boldsymbol{G} \) | is the control matrix |
In this example, we have a control variable \( \boldsymbol{u} \), which is based on the accelerometer measurement.
The system state \( \boldsymbol{x}_{n} \) is defined by:
\[ \boldsymbol{x}_{n} = \left[ \begin{matrix} x_{n} \\ \dot{x}_{n} \\ \end{matrix} \right] \]
Where:
- \( x_{n} \) is the rocket altitude at time \( n \)
- \( \dot{x}_{n} \) is the rocket velocity at time \( n \)
We can express the state extrapolation equation as follows:
\[ \left[ \begin{matrix} \hat{x}_{n+1,n}\\ \hat{\dot{x}}_{n+1,n}\\ \end{matrix} \right] = \left[ \begin{matrix} 1 & \Delta t \\ 0 & 1 \\ \end{matrix} \right] \left[ \begin{matrix} \hat{x}_{n,n}\\ \hat{\dot{x}}_{n,n}\\ \end{matrix} \right] + \left[ \begin{matrix} 0.5 \Delta t^{2} \\ \Delta t \\ \end{matrix} \right] \left( a_{n} + g \right) \]
In the above equation:
\[ \boldsymbol{F}= \left[ \begin{matrix} 1 & \Delta t \\ 0 & 1 \\ \end{matrix} \right] \]
\[ \boldsymbol{G}= \left[ \begin{matrix} 0.5 \Delta t^{2} \\ \Delta t \\ \end{matrix} \right] \]
\[ \boldsymbol{u}_{n} = \left( a_{n} + g \right) \]
The covariance extrapolation equation
The general form of the Covariance Extrapolation Equation is:
| \( \boldsymbol{P}_{n,n} \) | is the covariance matrix of the current state estimation |
| \( \boldsymbol{P}_{n+1,n} \) | is the covariance matrix of the next state estimation (prediction) |
| \( \boldsymbol{F} \) | is the state transition matrix that we derived in the "Modeling linear dynamic systems" section |
| \( \boldsymbol{Q} \) | is the process noise matrix |
The estimate covariance in matrix form is:
\[ \boldsymbol{P} = \left[ \begin{matrix} p_{x} & p_{x\dot{x}} \\ p_{\dot{x}x} & p_{\dot{x}} \\ \end{matrix} \right] \]
The elements of the main diagonal of the matrix are the variances of the estimation:
- \( p_{x} \) is the variance of the altitude estimation
- \( p_{\dot{x}} \) is the variance of the velocity estimation
- The off-diagonal entries are covariances
We have already derived the state transition matrix \( \boldsymbol{F} \). Now we shall derive the process noise \( \boldsymbol{Q} \) matrix.
The process noise matrix
We assume a discrete noise model - the noise is different at each time sample but is constant between time samples.
The process noise matrix for a constant acceleration model looks like this:
\[ \boldsymbol{Q} = \left[ \begin{matrix} \sigma_{x}^{2} & \sigma_{x\dot{x}}^{2} \\ \sigma_{\dot{x}x}^{2} & \sigma_{\dot{x}}^{2} \\ \end{matrix} \right] \]
We've already derived the Q matrix for the constant acceleration model. The Q matrix for our example is:
\[ \boldsymbol{Q} = \left[ \begin{matrix} \frac{\Delta t^{4}}{4} & \frac{\Delta t^{3}}{2} \\ \frac{\Delta t^{3}}{2} & \Delta t^{2} \\ \end{matrix} \right] \epsilon^{2} \]
Where:
- \( \Delta t \) is the time between successive measurements
- \( \epsilon^{2} \) is the random variance in accelerometer measurement
In the previous example, we used the system's random variance in acceleration \( \sigma_{a}^{2} \) as a multiplier of the process noise matrix. But here, we have an accelerometer that measures the system's random acceleration. The accelerometer error \( v \) is much lower than the system's random acceleration; therefore, we use \( \epsilon^{2} \) as a multiplier of the process noise matrix.
It makes our estimation uncertainty much lower!
Now we can write down the covariance extrapolation equation for our example:
Example analysis
The following chart compares the true, measured, and estimated values of the rocket altitude.
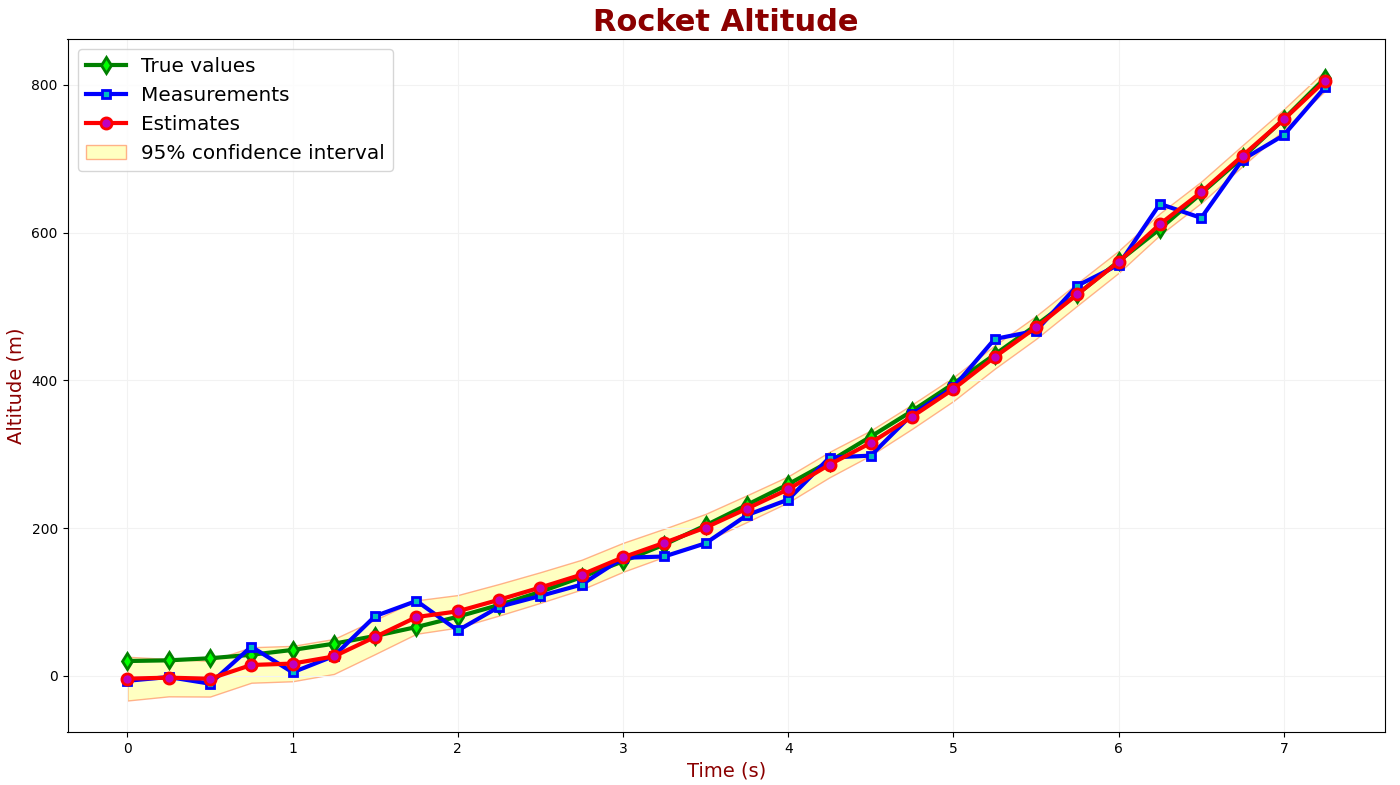
We can see a good KF tracking performance and convergence.
The following chart compares the true value, measured values, and estimates of the rocket velocity.
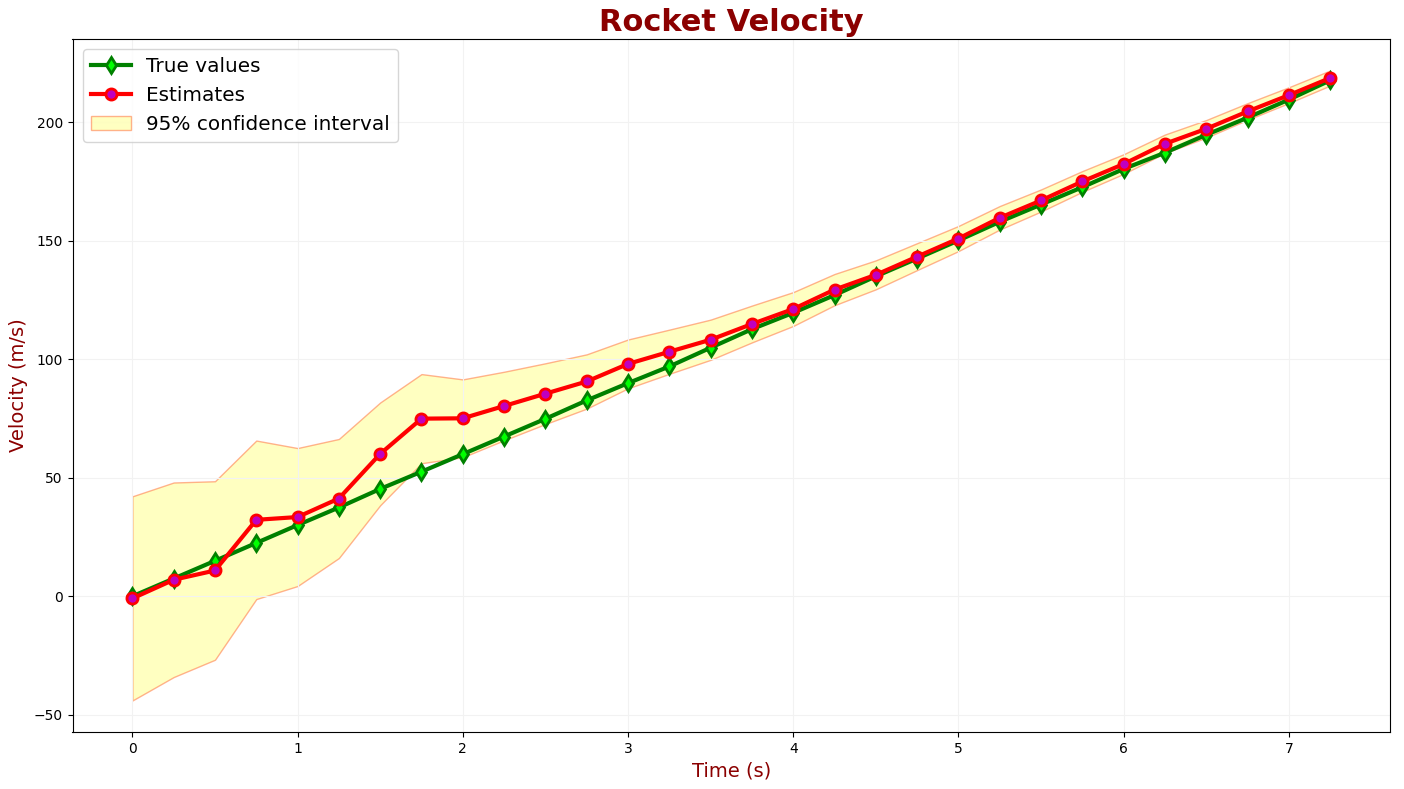
It takes about 2.5 seconds to converge the estimates to the true rocket velocity.
In the beginning, the estimated altitude is influenced by measurements, and it is not aligned well with the true rocket altitude since the measurements are very noisy.
But as the KF converges, the noisy measurement has less influence, and the estimated altitude is well aligned with the true altitude.
In this example, we don't have any maneuvers that cause acceleration changes, but if we had, the control input (accelerometer) would update the state extrapolation equation.
